Using light to control the properties of quantum materials not only holds the potential to realize new and interesting quantum many-body phases, but may also hold the key to create novel devices and functionalities. In most cases, this optical control is achieved by externally applying intense electromagnetic radiation to the system in question. Recently however, an appealing alternative route has been put forward which bypasses the need for intense external radiation. Instead ,one may attempt to use resonantly-coupled electromagnetic cavities to custom-tailor the properties of the electromagnetic vacuum-fluctuations directly.
A potentially powerful application of this approach is to use cavities to control antiferromagnetic correlations in a high-Tc cuprate superconductor. These correlations are believed to underlie many of the exotic, and potentially useful, aspects of the unconventional high-Tc superconductivity in these materials.
It therefore stands to reason that the ability to optically manipulate, and ultimately enhance, superconductivity in these materials is extremely appealing from both a theoretical and practical perspective, and may pave the way towards realizing room-temperature superconductivity—a “holy-grail” of modern condensed matter and material science. The concept of using cavities to manipulate superconductivity has already been put forward in the context of electron-phonon systems .
In this case, it has been proposed that strongly coupling resonant cavities to infrared-active optical phonons may offer away to manipulate the pairing between electrons in “conventional” superconductors. While indeed this may be a promising avenue towards achieving cavity-enhanced superconductivity, these systems still remain fundamentally limited by the relatively weak coupling strengths afforded by electron-phonon interaction.
In contrast, while the exact mechanism responsible for superconductivity in cuprates is still unclear, it is widely believed to be driven by interactions of electrons with spin-fluctuations rather than phonons. As a result, these systems have a higher “ceiling” for potential enhancement effects. At the same time it is also less clear how cavities may be used to modify these spin-fluctuations. Motivated by these considerations, we propose a scheme for realizing strong coupling of a resonant cavity to the spin fluctuations in an antiferromagnetic cuprate parent compound.
Cavity control of quantum matter may offer new ways to study and manipulate many-body systems. A particularly appealing idea is to use cavities to enhance superconductivity, especially in unconventional or high-Tc systems. Motivated by this, we propose a scheme for coupling Terahertz resonators to the antiferromagnetic fluctuations in a cuprate parent compound, which are believed to provide the glue for Cooper pairs in the superconducting phase.
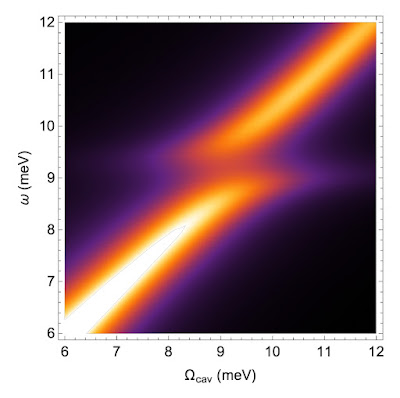
First, with derive the interaction between magnon excitations of the Ne´el-order and polar phonons associated with the planar oxygens. This mode also couples to the cavity electric field, and in the presence of spin-orbit interactions mediates a linear coupling between the cavity and magnons, forming hybridized magnon-polaritons. This hybridization vanishes linearly with photon momentum, implying the need for near-field optical methods, which we analyze within a simple model then derive a higher-order coupling between the cavity and magnons which is only present in bilayer systems, but does not rely on spin-orbit coupling. This interaction is found to be large, but only couples to the bimagnon operator.
As a result find a strong, but heavily damped, bimagnon-cavity interaction which produces highly asymmetric cavity line-shapes in the strong-coupling regime. To conclude, we outline several interesting extensions of our theory, including applications to carrier-doped cuprates and other strongly-correlated systems with Terahertz-scale magnetic excitations.
Overview of our proposal for forming cavity magnon-polaritons in insulating cuprates. (a) Depiction of the combined cavity-sample system. We consider placing the resonator on top of the cuprate (YBCO) sample, which is quasi-two dimensional and consists of layers of copper-oxide bilayers (for clarity we only depict the planar copper and oxygen atoms). The resonator produces a strong electric field (red arrows) which penetrates into the sample and couples to the magnons via the scheme outlined in Sec. II. (b) The phonon mode we consider in this paper, shown in a simplified depiction of the YBCO unit cell, is associated to the infrared-active motion of planar oxygens along the c-axis and strongly couples to both the cavity photons and the magnons in the cuprate. (c) Depiction of a typical split-ring resonator, which we use to model the Terahertz cavity in this work. Current flows through the metallic ring, inducing a magnetic field, as well as producing an electric field in the capacitive gap. (d) Cavity photon mode (gold) is constructed to lie close to the bottom of the magnon band (blue continuum), which are the two degrees we wish to couple to each other. The magnon-cavity coupling is mediated by virtual phonons, which both systems couple to directly. Because the phonon mode in question is higher in frequency than the relevant magnons and cavity, it can be adiabatically eliminated, yielding the desired cavity-magnon coupling.
reference :
S. Choi, J. Choi, R. Landig, G. Kucsko, H. Zhou, J. Isoya, F. Jelezko, S. Onoda, H. Sumiya, V. Khemani, C. v. Keyserlingk, N. Y. Yao, E. Demler, and M. D. Lukin, Observation of discrete time-crystalline order in a disordered dipolar many-body system, Nature (London) 543, 221 (2017).
M. Heyl, Dynamical quantum phase transitions: A review, Rep. Prog. Phys. 81, 054001 (2018).
Jonathan B. Curtis, Andrey Grankin, Nicholas R. Poniatowski, Victor M. Galitski, Prineha Narang, and Eugene Demler, Cavity magnon-polaritons in cuprate parent compounds, Cond-mat.str-el, (2021).